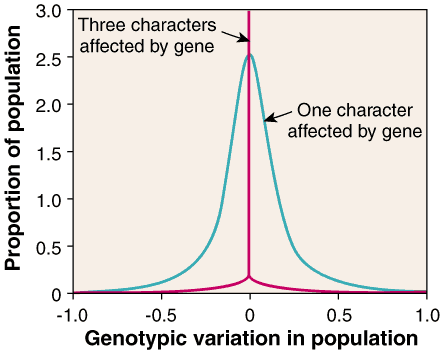
Evolutionary crystallization. As the number of characteristics affected by a gene increases from one (blue) to three (red), one genotype becomes dominant.
Are organisms like liquid droplets, infinitely malleable by the changing forces of evolution, or do they contain a "frozen core"--the Bauplan, or body design, which remains little changed under the varying adaptive pressures a lineage encounters during its history? Until quite recently, these questions have divided evolutionary biologists (as well as philosophers) into two almost non-overlapping camps. On the one hand are the so-called reductionists, largely recruited from the ranks of population genetics and associated disciplines, who are strongly committed to the adaptationist program of evolutionary biology. This group tends toward a world view in which there are no limits to an organism's variability and its ability to evolve. On the other hand are those biologists who primarily study whole organisms or complex phenotypic traits of organisms. This second group emphasizes the need to understand the constraints on evolutionary change that arise as a consequence of the intrinsic functional and developmental complexity of organisms. On page 1210 of this issue, Waxman and Peck (1) present a new mathematical result that reconciles most of the differences between these two camps. Population genetic equations predict, so they show, that parts of the phenotype effectively "crystallize" as the complexity of systems increase. But what is the problem to which this result is the solution?
The intellectual history of the problem goes back to the synthesis of Darwinian evolutionary theory and Mendelian genetics forged by the fathers of modern evolutionary theory, R. A. Fisher, S. Wright, and T. Dobzhansky. Through the marriage of genetics and Darwinism, it became clear that the process of evolution can be understood, or at least described, as changes in gene frequencies over time (2). New genes arise by mutation and are either lost (most likely) or they replace their parental genes, by selection or genetic drift. This, it turns out, is the most elementary level on which evolution can be explained. Consequently, a lot of effort was and continues to be invested in research directed at understanding these elementary processes. This remarkably successful research program has been pursued with the implicit assertion that evolution of real and complex organisms is just more of the same, and that no qualitatively new phenomena emerge as a result of increasing complexity (3). In this view, complexity is fundamentally irrelevant to an understanding of evolution. A corollary of this line of thinking is that all aspects and characters of the organism are variable and constantly changing (although at different rates), and the concept of a "Bauplan" (the body organization characteristic of a larger group of organisms) is an illusion (4).

Evolutionary
crystallization. As the number of characteristics affected by a gene
increases from one (blue) to three (red), one genotype becomes dominant.
A well-informed minority of organismal biologists, however, never were convinced of this radical view. Theirs is a more pluralistic view: yes, they agree, many characters are highly variable and their differences among species and populations can be understood as adaptations. But at some stages of evolution certain characters effectively "click in" and remain fixed in the descendent group of species (5-7). For instance, the chorda dorsalis (the embryonic precursor of our vertebral column) is absent in invertebrates, variably present in the relatives of vertebrates (ascidians and related groups) and absolutely fixed in vertebrates. The first who most clearly saw a connection between this pattern and increasing complexity was Rupert Riedl in the 1970s (6). He postulated that with increasing complexity some characters become more important because more and more new characters are functionally or developmentally predicated on them. Once such characters have accumulated many "responsibilities," mutational change will be detrimental and thus these characters become evolutionarily fixed. This increasing burden leads to fixation of characters. The problem with this view, however, was that it did not connect well with the then current population genetic theory.
Standard population genetic theory supports a liquid genome metaphor. In the balance between mutation and selection, each population settles into a state in which the most fit genotype is always surrounded by a sizable swarm of mutant genotypes buzzing around the best genotype (8), so much so that the concept of wild-type becomes meaningless. Variation is the name of the game. Only the amount of variation depends, in a continuous manner, on the relative strength of stabilizing selection, genetic drift, and mutation. Well, not exactly, according to the report by Waxman and Peck (1), which shows that there is a complexity limit beyond which genes can freeze into a fixed state and where the swarm of genetic variation suddenly disappears like fog in the sun. In the Waxman-Peck model, the complexity limit is reached once the genes affect more than two characters that are under simultaneous stabilizing selection.
To be precise, this freezing phenomenon has been described before (9), but it was seen as an arcane result of mathematical population genetics of uncertain significance and familiar to only a very few specialists. The significance of the present report is that Waxman and Peck have shown that this obscure property of mutation-selection equations has a connection to a generic property of organisms: complexity. Each gene has many effects and functions, each character is functionally connected to multiple others. Since this is the case, the freezing of genetic and phenotypic states is a necessary outcome, just as many organismal biologists have suspected for more than a century.
This sounds great and simple, but nothing in science is ever really simple. There is always the question whether the models are producing artifacts rather than pointing to fundamental insights. There is also no definite empirical proof as to whether the Bauplan concept is a perceptual artifact or a real pattern. Both are empirical questions that need to be settled. What makes the result by Waxman and Peck nonetheless exciting is that new emergent phenomena can be discovered that are not obvious from the study of simple models. More complexity is not just more of the same, but can lead to qualitatively new phenomena. This has long been know to physicists, but there are only a handful of examples where "complexity effects" were described in population genetic models (10). These and the report by Waxman and Peck show the need to study the population genetic theory of complex adaptations as a separate problem.